7 Significance of repeatability (r) and reproducibility (R)
7.1 General
The value of these quantities is estimated from analysis of variance (two-factor with replication) performed on the results obtained in a statistically designed inter-laboratory programme in which different laboratories each test a range of samples. Repeatability and reproducibility values shall be included in each published test method, and it is noted that the latter is usually greater than the former if the values are derived in accordance with this International Standard.
See in Annex H for an account of the statistical reasoning underlying the equations in this clause.
7.2 Repeatability, r
7.2.1 General
Most laboratories do not carry out more than one test on each sample for routine quality control purposes, except in abnormal circumstances, such as in cases of dispute or if the test operator wishes to confirm that his technique is satisfactory. In these abnormal circumstances, when multiple results are obtained, it is useful to check the consistency of repeated results against the repeatability of the method and the appropriate procedure is outlined in 7.2.2. It is also useful to know what degree of confidence can be placed on the average results, and the method of determining this is given in 7.2.3.
7.2.2 Acceptability of results
When only two results are obtained under repeatability conditions and their difference is less than or equal to r, the test operator may consider his work as being under control and may take the average of the two results as the estimated value of the property being tested.
If the two results differ by more than r, both shall be considered as suspect and at least three more results obtained. Including the first two, the difference between the most divergent result and the average of the remainder shall then be calculated and this difference compared with a new value, r1, instead of r, given in Equation (16):
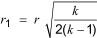
where k is the total number of results obtained.
If the difference is less than or equal to r1, all the results shall be accepted. If the difference exceeds r1, the most divergent result shall be rejected and the procedure specified in this subclause repeated until an acceptable set of results is obtained.
The average of the acceptable results shall be taken as the estimated value of the property. However, if two or more results from a total of not more than 20 have been rejected, the operating procedure and the apparatus shall be checked and a new series of tests made, if possible.
7.2.3 Confidence limits
When a single test operator, who is working within the precision limits of the method, obtains a series of k results under repeatability conditions, giving an average, X, it can be assumed with 95 % confidence that the true value, µ, of the characteristic lies within the following limits:
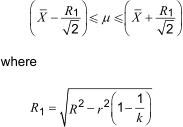
Similarly, for the single limit situation, when only one limit is fixed (upper or lower), it can be assumed with 95 % confidence that the true value, µ, of the characteristic is limited as follows:
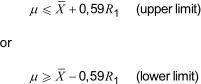
The factor 0.59 is the ratio 0.84/√2, where 0.84 is derived in Annex H.
However, since for most test methods r is much smaller than R, little improvement in the precision of the average is obtained by carrying out multiple testing under repeatability conditions.
If the reproducibility, R, of a test method has been found to be considerably greater than the repeatability, r, the reasons for the large value of the ratio R/r shall be analysed and the method, if possible, shall be improved.
7.3 Reproducibility, R
7.3.1 Acceptability of results
The procedure specified in this subclause is intended for judging the acceptability, with respect to the reproducibility of the test method, of results obtained by different laboratories in normal, day-to-day operations and transactions. In cases of dispute between a supplier and a recipient, the procedure specified in Clauses 8 to 10 shall be adopted.
When single results are obtained in two laboratories and their difference is less than or equal to R, the two results shall be considered as acceptable and their average, rather than either one separately, shall be considered as the estimated value of the tested property.
If the two results differ by more than R, both shall be considered as suspect. Each laboratory shall then obtain at least three other acceptable results (see 7.2.2).
In this case, the difference between the averages of all acceptable results of each laboratory shall be judged for conformity using a new value, R2, instead of R, as given by Equation (21):
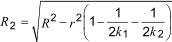
where
R is the reproducibility of the method;
r is the repeatability of the method;
k1 is the number of results of the first laboratory;
k2 is the number of results of the second laboratory.
If the difference between the averages is less than or equal to R2, then these averages are acceptable and their overall average shall be considered as the estimated value of the tested property. If the difference between the averages is greater than R2, then the procedure specified in Clauses 8 to 10 shall be adopted.
If circumstances arise in which (N + 1) > 2 laboratories each supply one or more acceptable results, the difference between the most divergent laboratory average and the average of the remaining N laboratory averages shall be compared to R3, where
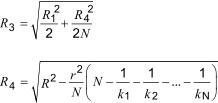
R1 is given in Equation (18), and corresponds to the most divergent laboratory average.
If this difference is equal to or less than R3 in absolute value, all results shall be regarded as acceptable and their average taken as the estimated value of the property.
If the difference is greater than R3, the most divergent laboratory average shall be rejected and the comparison using Equations (22) and (23) repeated until an acceptable set of laboratory averages is obtained. The average of these laboratory averages shall be taken as the estimated value of the property. However, if two or more laboratory averages from a total of not more than 20 have been rejected, the operating procedure and the apparatus shall be checked and a new series of tests made, if possible.
7.3.2 Confidence limits
When N laboratories obtain one or more results under conditions of repeatability and reproducibility, giving an average of laboratory averages X, it may be assumed with 95 % confidence that the true value µ of the characteristic lies within the following limits:
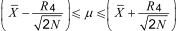
Similarly for the single limit situation, when only one limit is fixed (upper or lower), it may be assumed with 95 % confidence that the true value µ of the characteristic is limited as follows:
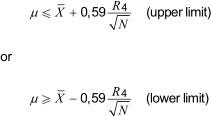
These equations also allow a given laboratory (N = 1) to determine the confidence level that can be assigned to the average of results by comparison with the true value.



