5 Inspection of inter-laboratory results for uniformity and for outliers
5.1 General
In 5.2 to 5.7, procedures are specified for examining the results reported in a statistically designed inter-laboratory programme (see Clause 4) in order to establish the following:
a) independence or dependence of precision and the level of results;
b) uniformity of precision from laboratory to laboratory;
c) and to detect the presence of outliers.
The procedures are described in mathematical terms based on the notation of Annex C and illustrated with reference to the example data (calculation of bromine number) set out in Annex D.
Throughout 5.2 to 5.7 (and Clause 6), the procedures used are first specified and then illustrated by a worked example using data given in Annex D.
It is assumed throughout this clause that all the results are either from a single normal distribution or capable of being transformed into such a distribution (see 5.2). Other cases (which are rare) require a different treatment that is beyond the scope of this International Standard. See Reference [8] for a statistical test on normality.
Although the procedures shown here are in a form suitable for hand calculation, it is strongly advised that an electronic computer with appropriately validated software be used to store and analyse inter-laboratory test results, based on the procedures of this International Standard (see, for example, Reference [9]).
5.2 Transformation of data
5.2.1 General
In many test methods, the precision depends on the level of the test result, and thus the variability of the reported results is different from sample to sample. The method of analysis outlined in this International Standard requires that this shall not be so and the position is rectified, if necessary, by a transformation.
The laboratories standard deviations, Dj, and the repeats standard deviations, dj, for sample j (see Annex C) are calculated and plotted separately against the sample means, mj. If the points so plotted can be considered as lying about a pair of lines parallel to the m-axis, then no transformation is necessary. If, however, the plotted points describe non-horizontal straight lines or curves of the form D = f1(m) and d = f2(m), then a transformation is necessary.
The relationships D = f1(m) and d = f2(m) are not, in general, identical. The statistical procedures of this International Standard require, however, that the same transformation be applicable both for repeatability and for reproducibility. For this reason, the two relationships are combined into a single dependency relationship D = f(m) (where D now includes d) by including a dummy variable, T. This takes account of the difference between the relationships, if one exists, and provides a means of testing for this difference (see Clause F.1).
The single relationship D = f(m) is best estimated by a weighted linear regression analysis, even though in most cases an unweighted regression gives a satisfactory approximation. The derivation of weights is described in Clause F.2, and the computational procedure for the regression analysis is described in Clause F.3. Typical forms of dependence D = f(m) are given in Clause E.1. These are all expressed in terms of transformation parameters B and B0.
The estimation of B and B0, and the transformation procedure which follows, are summarized in Clause E.2. This includes statistical tests for the significance of the regression (i.e. is the relationship D = f(m) parallel to the m-axis), and for the difference between the repeatability and reproducibility relationships, based at the 5 % significance level. If such a difference is found to exist, or if no suitable transformation exists, then the alternative sample-by-sample procedures of ISO 5725-2 shall be used. In such an event, it is not possible to test for laboratory bias over all samples (see 5.6) or separately estimate the interaction component of variance (see 6.2).
If it has been shown at the 5 % significance level that there is a significant regression of the form D = f(m), then the appropriate transformation y = F(x), where x is the reported result, is given by the equation:

where K is a constant. In that event, all results shall be transformed accordingly and the remainder of the analysis carried out in terms of the transformed results. Typical transformations are given in Clause E.1.
It is difficult to make the choice of transformation the subject of formalized rules. Qualified statistical assistance can be required in particular cases. The presence of outliers can affect judgement as to the type of transformation required, if any (see 5.7).
5.2.2 Worked example
Table 1 lists the values of m, D, and d for the eight samples in the example given in Annex D, correct to three significant digits. Corresponding degrees of freedom are in parentheses.
Inspection of the figures in Table 1 shows that both D and d increase with m, the rate of increase diminishing as m increases. A plot of these figures on log-log paper (i.e. a graph of log D and log d against log m) shows that the points may reasonably be considered as lying about two straight lines (see Figure F.1) From the example calculations given in Clause F.4, the gradients of these lines are shown to be the same, with an estimated value of 0.638. Bearing in mind the errors in this estimated value, the gradient may, for convenience, be taken as 2/3.
Hence, the same transformation is appropriate both for repeatability and reproducibility, and is given by the equation:

Since the constant multiplier may be ignored, the transformation thus reduces to that of taking the cube roots of the reported results (bromine numbers). This yields the transformed data shown in Table D.2, in which the cube roots are quoted correct to three decimal places.
5.3 Tests for outliers
5.3.1 General
The reported data, or if it has been decided that a transformation is necessary, the transformed results, shall be inspected for outliers. These are the values that are so different from the remaining data that it can only be concluded that they have arisen from some fault in the application of the test method or from testing a wrong sample. Many possible tests may be used and the associated significance levels varied, but those that are given below have been found to be appropriate for this International Standard. These outlier tests all assume a normal distribution of errors (see 5.1).
5.3.2 Uniformity of repeatability
5.3.2.1 General
The first outlier test is concerned with detecting a discordant result in a pair of repeat results. This test involves calculating the e2ij over all the laboratory/sample combinations. Cochran's criterion at the 1 % significance level is then used to test the ratio of the largest of these e2ij values over their sum (see Clause C.5). If its value exceeds the value given in Table D.3, corresponding to one degree of freedom, n being the number of pairs available for comparison, then the member of the pair farthest from the sample mean shall be rejected and the process repeated, reducing n by 1, until no more rejections are called for. In certain cases, this test "snowballs" and leads to an unacceptably large proportion of rejections (say more than 10 %). If this is so, this rejection test shall be abandoned and some or all of the rejected results shall be retained. An arbitrary decision based on judgement is necessary in this case.
5.3.2.2 Worked example
In the case of the example given in Annex D, the absolute differences (ranges) between transformed repeat results, i.e. of the pairs of numbers in Table D.2, in units of the third decimal place, are shown in Table 2.
The largest range is 0,078 for laboratory G on sample 3. The sum of squares of all the ranges is
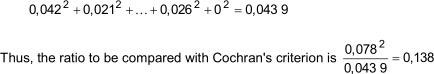
There are 72 ranges and, as from Table D.3, the criterion for 80 ranges is 0.1709, this ratio is not significant.
5.3.3 Uniformity of reproducibility
5.3.3.1 General
The following outlier tests are concerned with establishing uniformity in the reproducibility estimate and are designed to detect either a discordant pair of results from a laboratory on a particular sample or a discordant set of results from a laboratory on all samples. For both purposes, the Hawkins' test is appropriate.
This involves forming for each sample, and finally for the overall laboratory averages (see 5.6), the ratio of the largest absolute deviation of laboratory mean from sample (or overall) mean to the square root of certain sums of squares (see Clause C.6).
The ratio corresponding to the largest absolute deviation shall be compared with the critical 1 % values given in Table D.4, where n is the number of laboratory/sample cells in the sample (or the number of overall laboratory means) concerned and where v is the degrees of freedom for the sum of squares, which is additional to that corresponding to the sample in question. In the test for laboratory/sample cells, v refers to other samples, but is zero in the test for overall laboratory averages.
If a significant value is encountered for individual samples, the corresponding extreme values shall be omitted and the process repeated. If any extreme values are found in the laboratory totals, then all the results from that laboratory shall be rejected.
If the test "snowballs", leading to an unacceptably large proportion of rejections (say more than 10 %), then this rejection test shall be abandoned and some or all of the rejected results shall be retained. An arbitrary decision based on judgement is necessary in this case.
5.3.3.2 Worked example
The application of Hawkins' test to cell means within samples is shown below.
The first step is to calculate the deviations of cell means from respective sample means over the whole array. These are shown in Table 3, in units of the third decimal place.
The sum of squares of the deviations are then calculated for each sample. These are also shown in Table 3 in units of the third decimal place.
The cell tested is the one with the most extreme deviation. This was obtained by laboratory D from sample 1. The appropriate Hawkins' test ratio is therefore

The critical value, corresponding to n = 9 cells in sample 1 and v = 56 extra degrees of freedom from the other samples, is interpolated from Table D.4 as 0.3729. The test value is greater than the critical value and so the results from laboratory D on sample 1 are rejected.
As there has been a rejection, the mean value, deviations and sum of squares are recalculated for sample 1, and the procedure is repeated. The next cell to be tested is that obtained by laboratory F from sample 2. The Hawkins' test ratio for this cell is:
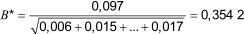
The critical value corresponding to n = 9 cells in sample 2 and v = 55 extra degrees of freedom is interpolated from Table D.4 as 0.3756. As the test ratio is less than the critical value, there are no further rejections.
5.4 Rejection of complete data from a sample
5.4.1 General
The laboratories standard deviation and repeats standard deviation shall be examined for any outlying samples. If a transformation has been carried out or any rejection made, new standard deviations shall be calculated.
If the standard deviation for any sample is excessively large, it shall be examined with a view to rejecting the results from that sample.
Cochran's criterion at the 1 % level can be used when the standard deviations are based on the same number of degrees of freedom. This involves calculating the ratio of the largest of the corresponding sums of squares (laboratories or repeats, as appropriate) to their total (see Clause C.5). If the ratio exceeds the critical value given in Table D.3, with n as the number of samples and ν the degrees of freedom, then all the results from the sample in question shall be rejected. In such an event, care should be taken that the extreme standard deviation is not due to the application of an inappropriate transformation (see 5.2), or undetected outliers.
There is no optimal test when standard deviations are based on different degrees of freedom. However, the ratio of the largest variance to that pooled from the remaining samples follows an F-distribution with v1 and v2 degrees of freedom (see Clause C.7). Here v1 is the degrees of freedom of the variance in question and v2 is the degrees of freedom for the remaining samples. If the ratio is greater than the critical value given in Tables D.6 to D.10, corresponding to a significance level of 0.01/S, where S is the number of samples, then results from the sample in question shall be rejected.
5.4.2 Worked example
The standard deviations of the transformed results, after the rejection of the pair of results by laboratory D on sample 1, are given in Table 4 in ascending order of sample mean, correct to three significant digits. Corresponding degrees of freedom are in parentheses.
Inspection shows that there is no outlying sample amongst these. It is noted that the standard deviations are now independent of the sample means, which was the purpose of transforming the results.
The figures in Table 5, taken from a test programme on bromine numbers over 100, illustrate the case of a sample rejection.
It is clear, by inspection, that the laboratories' standard deviation for sample 93 at 15.26 is far greater than the others. It is noted that the repeats standard deviation in this sample is correspondingly large.
Since laboratory degrees of freedom are not the same over all samples, the variance ratio test is used. The variance pooled from all samples excluding sample 93 is the sum of the sums of squares divided by the total degrees of freedom, that is:
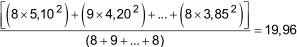
The variance ratio is then calculated as (15.26(2))/19.96 = 11.66.
From Tables D.6 to D.10, the critical value corresponding to a significance level of 0.01/8 = 0.00125, for 8 and 63 degrees of freedom, is approximately 4. This is less than the test ratio and results from sample 93 shall. therefore, be rejected.
Turning to repeats standard deviations, it is noted that degrees of freedom are identical for each sample and that Cochran's test can therefore be applied. Cochran's criterion is the ratio of the largest sum of squares (sample 93) to the sum of all the sums of squares, that is:
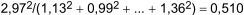
This is greater than the critical value of 0.352 corresponding to n = 8 and v = 8 (see Table D.3), and confirms that results from sample 93 shall be rejected.
5.5 Estimating missing or rejected values
5.5.1 One of the two repeat values missing or rejected
If one of a pair of repeats (yij1 or yij2) is missing or rejected, this shall be considered to have the same value as the other repeat in accordance with the least squares method.
5.5.2 Both repeat values missing or rejected
5.5.2.1 General
If both the repeat values are missing, estimates of aij (= yij1 + yij2) shall be made by forming the laboratories x samples interaction sum of squares, including the missing values of the totals of the laboratories/samples pairs of results as unknown variables. Any laboratory or sample from which all the results were rejected shall be ignored and new values of L and S used. The estimates of the missing or rejected values shall then be found by forming the partial derivatives of this sum of squares with respect to each variable in turn and equating these to zero to solve as a set of simultaneous equations.
Equation (4) may be used where only one pair sum has to be estimated. If more estimates are to be made, the technique of successive approximation can be used. In this, each pair sum is estimated in turn from Equation (4), using L1, S1 and T1 values which contain the latest estimates of the other missing pairs. Initial values for estimates can be based on the appropriate sample mean, and the process usually converges to the required level of accuracy within three complete iterations. See, for instance, Reference [5] in the bibliography for details.
If the value of one pair sum, a ij , has to be estimated, the estimate is given by Equation (4):
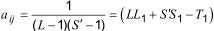
where
S' is S minus the number of samples rejected in 5.4;
L1 is the total of remaining pairs in the ith laboratory;
S1 is the total of remaining pairs in the jth sample;
T1 is the total of all pairs except aij.
5.5.2.2 Worked example
The two results from laboratory D on sample 1 were rejected (see 5.3.3) and thus aij has to be estimated.
total of remaining results in laboratory 4 = 36.354;
total of remaining results in sample 1 = 19.845;
total of all the results except aij = 348.358.
Also S' = 8 and L = 9.
Hence, the estimate of aij, is given by
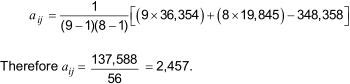
5.6 Rejection test for outlying laboratories
5.6.1 General
At this stage, one further rejection test remains to be carried out. This determines whether it is necessary to reject the complete set of results from any particular laboratory. It cannot be carried out at an earlier stage, except in the case where no individual results or pairs are missing or rejected. The procedure, again, consists of Hawkins' test (see 5.3.3), applied to the laboratory averages over all samples, with any estimated results included. If any laboratories are rejected on all samples, new estimates shall be calculated for any remaining missing values (see 5.5).
5.6.2 Worked example
The procedure on the laboratory averages shown in Table 6 below follows exactly that specified in 5.3.3.
The deviations of laboratory averages from the overall mean are given in Table 7 in units of the fourth decimal place, together with the sum of squares.
Hawkins' test ratio is, therefore,

Comparison with the value tabulated in Table D.4, for n = 9 and v = 0, shows that this ratio is not significant and, therefore, no complete laboratory rejections are necessary.
5.7 Confirmation of selected transformation
5.7.1 General
At this stage, it is necessary to check that the rejections carried out have not invalidated the transformation used. If necessary, the procedure given in 5.2 shall be repeated with the outliers deleted, and if a new transformation is selected, outlier tests shall be re-applied.
5.7.2 Worked example
It is not considered necessary in this case to repeat the calculations from 5.2 with the outlying pair deleted.



