7. Procedure
7.1 The flow rate of the combination agitator and temperature control device should be between 3500 and 4500 mL/min. The flow rate should be measured with a piece of 6.35-mm inside diameter bore plastic tubing temporarily attached to the pump outlet and removed after this measurement. During the test, do not use attachments such as tubing, stopcocks, pinch clamps, etc. on the pump outlet.
7.2 Add 4275 mL of test water to the beaker, install the agitator-temperature control device, and adjust it for 60°C temperature. When the water reaches this temperature, add 225 mL of the rolling oil to be tested. (The oil sample should be sufficiently agitated to assure complete mixing of oil components. With most materials, sufficient heat to melt all of the components will also be required, however, at no time should the temperature exceed 60°C.) Continue controlled temperature agitation for 30 min.
7.3 While agitation continues, fill one Babcock bottle for an emulsion concentration control test, as follows: Open the pinch clamp on the beaker sample tap for 2 to 3 s. Discard about 20 mL of emulsion to flush the tap, and attempt to come as cleanly as possible to the end. Close the pinch clamp, place the hose tip in a Babcock bottle, and fill it at a rapid flow rate to the 50-mL mark.
7.4 Stop agitation and re-start the stop watch at zero time. Fill Babcock bottles as described above at 30 s and 1, 2, 4, 8, 16, and 32 min elapsed time. It is permissable to stop sampling sooner or later (such as at 16 or 64 min) if such data are desired, but earlier sample times may not be omitted even for very stable emulsions, because the sampling process slightly affects further settling rates. For each sample, purge the sample tap several seconds ahead of time so that filling the Babcock bottle starts at the correct time.
7.5 Fill each Babcock bottle to the upper graduation line with 30 vol% sulfuric acid. Swirl while filling. Spin in the centrifuge for 10 min, or until a clean separation is obtained. It may be necessary to use a different mineral acid or to heat the filled Babcock bottles to facilitate a clean separation. (If however, none of these methods results in a clean separation, the test method cannot be considered applicable for that particular oil.) Read the difference in levels in terms of the Babcock bottle calibration scale at the top and bottom of the oil layer.
8. Calculation
8.1 For the sample bottle taken as a control during agitation, calculate the percent of oil found. Since the calibrations on the neck of the Babcock bottle usually range from 0 to 50, and correspond to 10 % oil in this test method, the difference in scale reading between the top and bottom of the oil layer divided by 5 equals the percent oil. If this result is not close to 5 %, the results are suspect until repeat runs verify the reproducibility of the discrepancy. Significant amounts of water soluble compounds in the oil sample might explain low concentrations, for example. If, by the end of the 30 min agitation period, any significant amount of free oil or inverted emulsion remains floating on the surface without being repeatedly drawn down into the water layer, the oil is probably too difficult to disperse for the test method to be applicable.
8.2 For each sample taken after agitation was stopped, calculate the amount of oil found as a percent of the amount found in the sample.
8.3 A single number used to describe the rolling oil emulsion stability is the slope of a straight line, fit by the method of least squares, to the base ten logarithms of both time, in minutes, and the measured concentrations in percent. In practice, to avoid taking the of zero, use the concentration plus 1 %.
8.4 The estimate of the Slope b, for an experimental trial is easily obtained by completing the following worksheet.
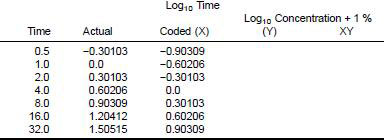
8.5 Enter the log of the test result plus 1 on the appropriate line. Form the product of each coded time (X) and the corresponding concentration (Y). Add the seven resulting values. The slope is then calculated by the following formula:
b = ΣXY/2.53733

